【顧客流失預測項目】2. 模型會長怎樣
系列回顧
建構模型
當我們終於對手上的數據有一個算詳細的認知後,是時候開始建構我們的預測模型。這次的問題是一個分類問題,把顧客按他的資料分為「會離開」跟「不會離開」。不過世上分類模型何其多,我們該用哪一個呢?
另外是否有必要把全部的特徵都用上呢?會不會有辦法用一部分特徵就已經可以有很好的表現呢?
而最後我們的預測模型又表現如何?是否可以加以調整,讓它表現更好呢?
這三大問題,就是我們今天要來處理的事啦!
建構前處理
在選擇用甚麼模型、特徵前,我們還有一些數據預處理的事情要解決,想想都頭痛(不是),那我們很快的看一下吧。完整過程可以到我的 GitHub 或 Kaggle 上瀏覽。
在訓練分類模型上,我們可以把它當成一個甚麼都不懂的小孩,
1. 拆分訓練、測試資料集
為了在教完分類模型東西後,可以評估它的表現,我們可以把現有的資料集拆分為兩組(訓練組&測試組),那麼就可以用訓練組的資料去教會我們的模型如何去分類,然後就把它未見過的測試組當成試題,要它答題做卷,再把它的預測跟我們有的答案對一對,自然知道它的表現如何。
from sklearn.model_selection import train_test_split X = data.drop(['Churn'], axis=1) y = data["Churn"] # test/train generally = 0.2/0.8 or 0.3/0.7 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=42, stratify=data["Churn"])
2. 處理不平衡數據
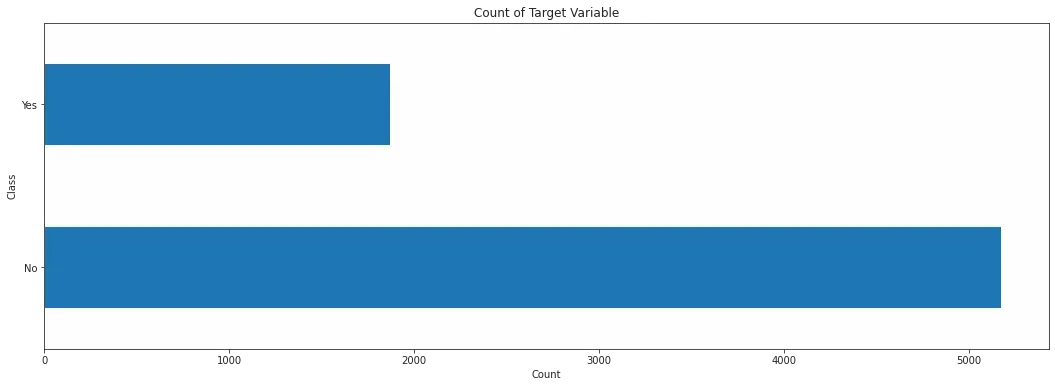
那麼為甚麼要處理不平衡數據?比如說,如果我們教了模型100 題,當中95 題的答案是A,只有5 題的的答案是B,那麼為甚麼它還要嘗試學習A 跟 B 的分別?反正這個老師出的材料都是A 的偏多,模型全都答A 不就搞定!!EASY!! (不是)
為了避免這種情況,更好的教會我們的模型如何分辨A 跟 B,我們當然要想辦法以同樣比例去教 A 跟 B 。但是考卷還是要記得貼近現實的情況,不然只學會課上的東西,不會處理現實的情境也沒用嘛。所以處理我們這裡只會處理訓練組的不平衡問題,測試組的就放著吧。
# SMOTEENN = SMOTE + ENN from imblearn.combine import SMOTEENN sm = SMOTEENN() X_train_resampled, y_train_resampled = sm.fit_sample(X_train, y_train)
選擇模型
準備好數據,就可以開始建構模型了。不過分類模型那麼多,我們該如何去選擇用哪一個呢,那麼不如比較一下各個分類模型,然後就用表現比較好的那一個吧。
所以這裡我們會測試一堆分類模型,然後就挑出表現好的模型來用。但我又懶,所以我用了一個External Library lazypredict 幫我完成這個部分。只要簡單幾行代碼,它就會自動幫我把一堆分類模型的基本表現算出來。
#!pip install lazypredict import lazypredict from lazypredict.Supervised import LazyClassifier clf = LazyClassifier(verbose=0, ignore_warnings=True, custom_metric=None) models, predictions = clf.fit(X_train_resampled, X_test, y_train_resampled, y_test) print(models)
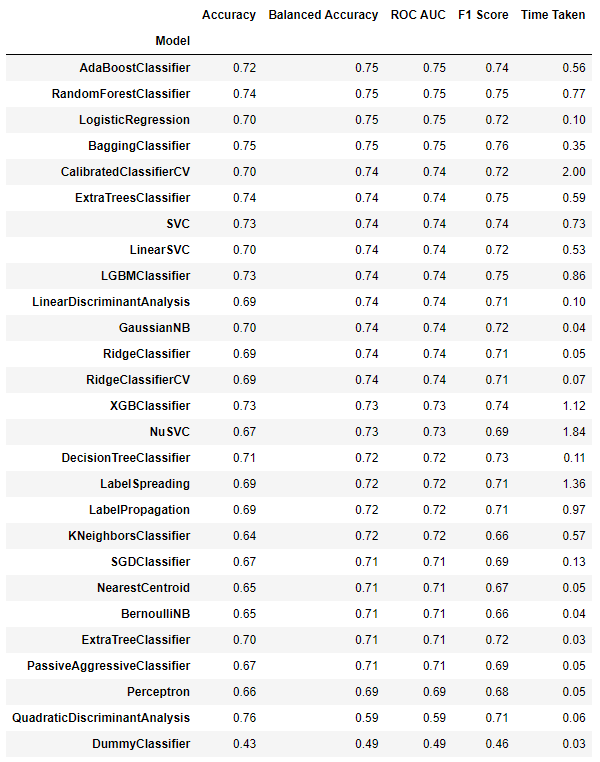
從 Lazypredict 給我們的結果,看起來 AdaBoost Classifier, Random Forest Classifier, Logistic Regression, Bagging Classifier 都表現不錯,不過我們先從我熟悉的 Random Forest Classifier 開始吧(得從一個自己最理解背後在發生甚麼的模型開始,不然就不用你選了機器全給你做好了)。
建立基本版的Random Forest Classifier
建立一個基礎模型有助我們去對比調參後模型的表現,也可以 在調參多次失敗後心很累不想做時 之後萬一出了問題,能夠用回最基礎的模型。
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import *
base_rf = RandomForestClassifier(n_estimators=200, random_state = 100)
base_rf.fit(X_train_resampled, y_train_resampled)
y_pred = base_rf.predict(X_test)
print(f"Model base score: {base_rf.score(X_test, y_test):.4}\\n")
# print(classification_report(y_test, y_pred, labels=[0,1]))
Model base score: 0.7392
precision recall f1-score support
0 0.90 0.73 0.80 1033
1 0.51 0.78 0.61 374
accuracy 0.74 1407
macro avg 0.70 0.75 0.71 1407
weighted avg 0.80 0.74 0.75 1407
從以上可見,我們的基礎模型(用盡了所有特徵&未進行參數調整),在測試中得到73.92%的準確率,準確率是指猜中0+猜中1的比率。(0是不離開,1是離開)

我們可以再細化一下猜錯的部分。在猜錯的部分主要分為兩種情況,分別是「我們猜他會離開,誰知道他留下了」(走運的猜錯),以及「我們猜他會留下,誰知道他離開了」(看走眼出事了)。看走眼的那一部分在這裡是False Negative (FN),而 Recall 正是一個關注這部分的分數,所以之後,我們會更為關注 Recall 的分數表現。有關Confusion Martrix、Recall 等更多說明,可以看這篇文章,作者的解說及例子十分詳細。
事實上,我們的現實情況其實是不平衡的,單看準確率並不足夠,因為準確率並不能告訴我們成功認出多少個更重要的少數項,所以我們反而要更關注Recall。這裡不是說我們不用關注模型可以成功猜對多少個答案,不過因為我們這次項目主要是希望找出那些預測起來可能會離開的客戶,然後進行後續行動,所以應該寧濫勿缺,要模型可以成功猜中更多會離開的顧客,以及更重要的減少錯誤預測會離開的客戶為不會離開,而錯過行動的機會。
特徵選取
當我們決定好了用哪一個模型、如何去評估模型表現後,下一步就是想一想到底用多少個特徵。如果用一部分的特徵就可以得到跟用全部特徵差不多的準確度,我們為什麼要浪費額外的算力呢?
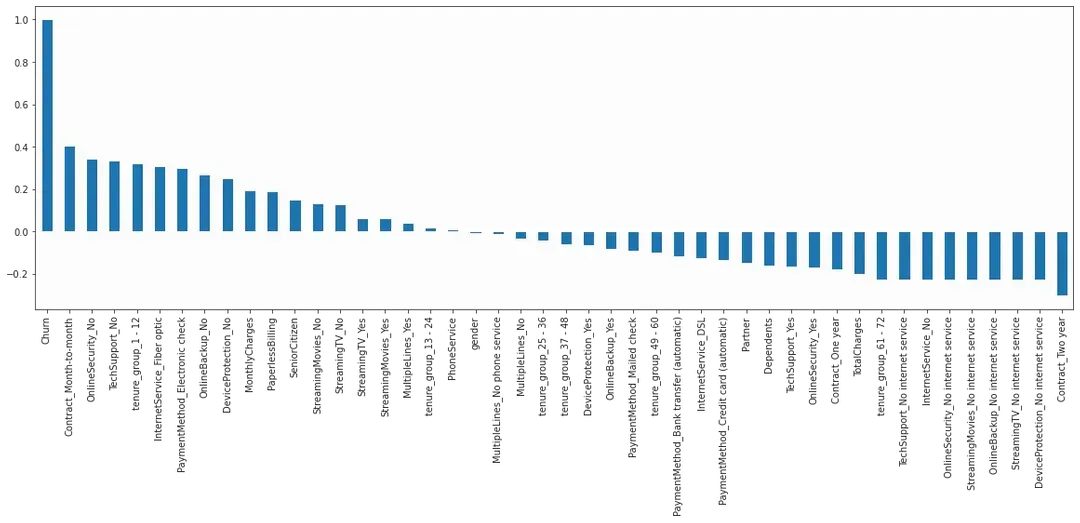
而有關要用多少個,又或者用哪些特徵,其實我們之前就已那麼回答了這個問題,在找尋最能反映顧客離開的特徵時,我們就已經調一個 correlation ,以及用Random Forest Classifier 把Features Improtances算了出來,那麼我們先重溫一下。
plt.figure(figsize=(20,6)) data_dummies.corr()['Churn'].sort_values(ascending = False).plot(kind='bar')
feature_select = RandomForestClassifier() feature_select = feature_select.fit(X_train_resampled, y_train_resampled) importances = feature_select.feature_importances_ # into dataframe feature_importance = zip(X_train.columns, importances) feature_importance_df = pd.DataFrame(feature_importance, columns =['Features', 'Importances']) feature_importance_df.sort_values(by="Importances",inplace=True,ascending=False) # In barchart plt.figure(figsize=(10,6)) sns.barplot(x = "Importances", y ="Features", data = feature_importance_df.head(15))
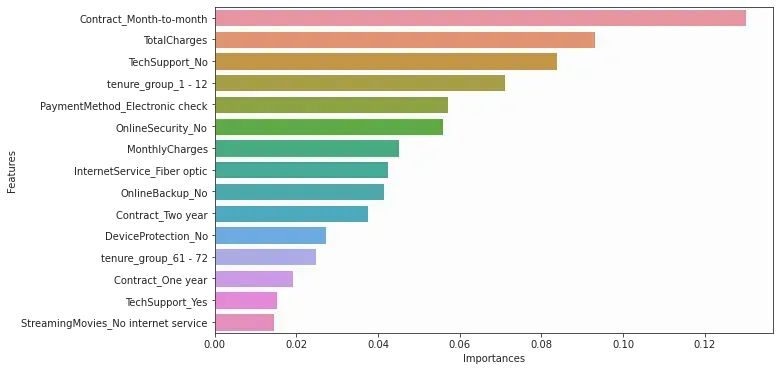
由上圖可見,每月續約、總費用、沒有使用附加服務、餘下合約期在一年內、以電子支票作支付,每月費用,使用光纖服務 都與 顧客是否離開 有較大關係。而這些特徵,都是我們的模型應該優先學習的東西。那麼下一個問題就是,我們模型要學習多少個最有關連特徵。關於這個問題,這裡比較簡單,我們簡單粗暴的直接測試用 5 個最有關連的特徵以及用 10 個最有關連的特徵,再去比較它們的表現。當然也可以把使用 1 至 15 個特徵的分數全算出來。
Function - 幫助我們取得 n 個最有關連的特徵
def get_feature_list(n): l = [] for x in feature_importance_df.head(n).Features: l.append(x) return l
5 個最有關連的特徵
select_features_5 = get_feature_list(5)
X_select5 = data[select_features_5]
y = data["Churn"]
X_train_select5, X_test_select5, y_train, y_test = train_test_split(X_select5, y, test_size = 0.2, random_state=42, stratify=data["Churn"])
X_train_select5_resampled, y_train_resampled = sm.fit_sample(X_train_select5,y_train)
rf_select5 = RandomForestClassifier(n_estimators=200, criterion='gini', random_state = 100)
base_rf.fit(X_train_select5_resampled, y_train_resampled)
y_pred_select5 = base_rf.predict(X_test_select5)
print(classification_report(y_test, y_pred_select5))
print("\\nScore of test data:")
print(f" Mean Accuracy :{base_rf.score(X_test_select5, y_test):.4}")
print(f" F1 score :{f1_score(y_test, y_pred_select5):.4}")
print(f" Precision score :{precision_score(y_test, y_pred_select5):.4}")
print(f"*Recall score* :{recall_score(y_test, y_pred_select5):.4}")
precision recall f1-score support
0 0.85 0.75 0.79 1033
1 0.47 0.62 0.54 374
accuracy 0.71 1407
macro avg 0.66 0.69 0.67 1407
weighted avg 0.75 0.71 0.73 1407
Score of test data:
Mean Accuracy :0.715
F1 score :0.5375
Precision score :0.4726
*Recall score* :0.623
10 個最有關連的特徵
select_features_10 = get_feature_list(10)
X_select10 = data[select_features_10]
y = data["Churn"]
X_train_select10, X_test_select10, y_train, y_test = train_test_split(X_select10, y, test_size = 0.2, random_state=42, stratify=data["Churn"])
X_train_select10_resampled, y_train_resampled = sm.fit_sample(X_train_select10,y_train)
rf_select5 = RandomForestClassifier(n_estimators=200, criterion='gini', random_state = 100)
base_rf.fit(X_train_select10_resampled, y_train_resampled)
y_pred_select10 = base_rf.predict(X_test_select10)
print(classification_report(y_test, y_pred_select10))
print("\\nScore of test data:")
print(f" Mean Accuracy :{base_rf.score(X_test_select10, y_test):.4}")
print(f" F1 score :{f1_score(y_test, y_pred_select10):.4}")
print(f" Precision score :{precision_score(y_test, y_pred_select10):.4}")
print(f"*Recall score* :{recall_score(y_test, y_pred_select10):.4}")
precision recall f1-score support
0 0.87 0.77 0.82 1033
1 0.52 0.68 0.59 374
accuracy 0.74 1407
macro avg 0.69 0.72 0.70 1407
weighted avg 0.78 0.74 0.75 1407
Score of test data:
Mean Accuracy :0.7448
F1 score :0.5869
Precision score :0.5152
*Recall score* :0.6818
從以上可見,選取10 個最有關連的特徵而建立的模型可以達到一個與基礎模型接近的準確率,以及比選取5 個特徵的模型更高的Recall分數,這裡就先選取10 個最有關連的特徵去建立我們的模型吧。
不過選取10 個最有關連的特徵而建立的模型的Recall分數沒有基礎模型好,看來我們要調整參數去改善它的表現。
調整參數(Hyperparameter-tuning)
為了找到最好參數,我們會用上GridSearch,簡單來說就是暴力地把所有我們想試的參數組合全都算一遍,然後找出當中最好的那一組。事實上我做了三部分GridSearch 去尋找最優參數,慢慢縮小範圍,以下只是最後一次的GridSearch,完整過程可以到我的 GitHub 或 Kaggle 上瀏覽。
base_rf = RandomForestClassifier(n_estimators=200, random_state = 100)
from sklearn.model_selection import GridSearchCV
param_grid_2 = {"n_estimators": [200,225,250,300,325,350],# 森林中有多少顆樹
"max_depth": [1,2], # 最多可以有多少屠
"min_samples_leaf": [3,5,7], # 每個節點所需的最小樣本數量。
"bootstrap": [True, False]}
grid_search_forest_2 = GridSearchCV(base_rf,
param_grid_2,
cv = 3, # 做 3次 cross validation
scoring = "recall",
n_jobs=-1, # CPU 全開
verbose=3) # 顯示進程
grid_search_forest_2.fit(X_train_select10_resampled, y_train_resampled)
print(grid_search_forest_2.best_estimator_)
print(f"\\nThe trained recall score: {grid_search_forest_2.best_score_:.4f}\\n")
RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None, criterion='gini', max_depth=1, max_features='auto', max_leaf_nodes=None, max_samples=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=3, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=350, n_jobs=None, oob_score=False, random_state=100, verbose=0, warm_start=False) The trained recall score: 0.9462
當我們找到最好表現的那一組參數後,就可以用來建構我們的最終模型,
# since it is test data set
best_model = grid_search_forest_2.best_estimator_
y_pred = best_model.predict(X_test_select10)
print(classification_report(y_test, y_pred))
print("\\nScore of test data:")
print(f" Mean Accuracy :{base_rf.score(X_test_select10, y_test):.4}")
print(f" F1 score :{f1_score(y_test, y_pred):.4}")
print(f" Precision score :{precision_score(y_test, y_pred):.4}")
print(f"*Recall score* :{recall_score(y_test, y_pred):.4}")
precision recall f1-score support
0 0.91 0.63 0.74 1033
1 0.45 0.82 0.58 374
accuracy 0.68 1407
macro avg 0.68 0.73 0.66 1407
weighted avg 0.78 0.68 0.70 1407
Score of test data:
Mean Accuracy :0.7448
F1 score :0.5784
Precision score :0.4457
*Recall score* :0.8235
模型表現

到最後就是要看一看分數去比對一下我們的模型表現。上圖把基礎模型、選用 5 個最有關連特徵的模型、選用 10 個最有關連特徵的模型、選用 10 個最有關連特徵的模型(調參後)的分數表現。可以看到在準確性上,調參後的模型分數與基礎模型相差不遠,但在Recall 上表現的很好。代表我們成功減少誤判會離開的客戶為不離開的數字。
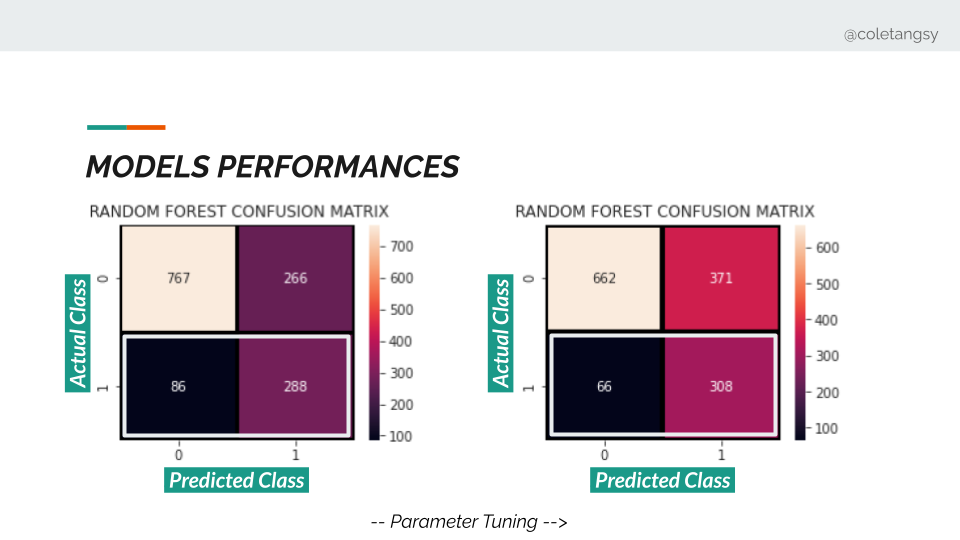
我們可以再看基礎模型以及調參後的模型的Cunfusion Matrix,可以看到的確成功減少誤判會離開的客戶為不離開的黑色區域數字,增加了成功判定會離開的顧客的數字。不過代價是在判定會留下的顧客的準確度上會有所下降,因為我們採取了一個寧殺錯,不放過的策略。
在成本上來說,據說開發一個新客戶的成本比挽留一個棍離開的舊客戶可以高上7倍左右。
換言之,說不定我多花一點在挽留客戶上,成本也沒有開發一個新客戶的高。不過可能對於這間電訊公司來說,提升光纖服務的品質,也會起到與這種顧客關係維繫策略類似的效果。(笑)
目前我們分析過手上的數據,也建立好預測模型,最後一步就是準備一個簡單的版本(上線),可以讓銷售、客戶服務同事可以快速的輸入了客戶資料,從而決定策略。讓這個預測模型不只是後台同事的 玩具 工具,前線同事也可以應用起來(雖然只是internal deployment 仍沒上雲端....)
各種聯繫方法目前應該包括:
