對雲端發票抽獎爭議的反思
關於雲端發票的抽獎活動,最近在台灣引發熱議,對此嘗試用不同的角度來看待這件事情。
兩道數學考題,看似簡單卻是難。歡迎來挑戰
兩道有關機率的問題,問題很簡單,但能想出正確答案,一點都不簡單。
【小說】秘密生活(33)
英敬說:「如果是這樣,我更要出乎同學意料,好呀!我報名參加新聞營。」他的回答真的讓素華很意外,一定也會讓班上多數同學很意外吧!

為什麼信心水準不是機率?
這是很多統計學初學者會有的疑惑。大部分的統計數據呈現,像是人口調查、民調等等,都會利用抽樣來推估真實值,並在抽樣的結果附近加上一段信賴區間,可以簡單理解為誤差範圍(如果涉及統計推論則會呈現 p 值)。那個範圍會有他對應的信心水準,但很多人將其理解為「真實值落在這個範圍內的機率」,然而這其實是錯誤的。
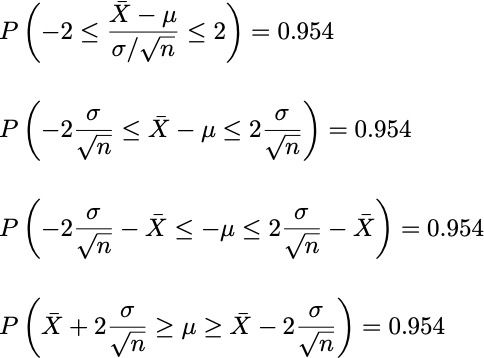
季節病
其實根本沒有無奇不有之說,只有事情的發生機率與貝式定理的命定與隨機,增加或減少某些作為就是減少或增加每件隨之而來的事情發生機率罷了。

什麼是賭
好賭不是壞事

目標要能立即記起重點的讀書筆記-高勝算決策,Annie Duke
不能以結果來判斷決策的正確性

機率不是這樣算的
從笑話中看數學~

《高勝算決策》運用下注思維,打敗三個大魔王
轉換為服膺於機率的視角,事前(信念)講究信心水準,(決策)過程中擁抱不確定性,事後(從結果)挖掘出學習機會。

【電影.《I, Robot》】光有理性不夠,還要有人性
只談機率還不夠,人類還有一個思考模式

條件機率 vs 聯合機率
花十分鐘搞懂「條件機率」與「聯合機率」的差別!

原來「機率」是這麼一回事!
「機率」是平易近人的觀念,日常生活中隨處可見的知識!本文希望不要涉入太多數學與理論,用簡單、生活化的例子闡述機率的概念。再給自己一次了解「機率」的機會 💪🏻

Bayesian機率
只要是估算,就會有誤差,因此投資者應該與「不確定」和平共處,而不是夢想找到一個完美神準模型。

【書】Rock Breaks Scissors《為什麼出布容易贏》
剪刀、石頭、布」是我們耳熟能詳的猜拳遊戲,理論上出剪頭、石頭跟布的機率應該各佔 1/3 ,也因此當我們無法做出決定時,往往會藉由這看似憑藉運氣的遊戲來做出決定。但根據統計,即使只出一拳也有勝率比較高的策略。除了猜拳遊戲之外、「隨機」的概念可能與我們所想像中有很大的出入,本書便探討運動賽事、考試出題、股票市場等等許多看…

202.你可能只是亂槍打鳥,請別往臉上貼金
今天要談相當經典的例子:德州神槍手謬誤 當結果看似有意義,或你希望某個偶發事件具有意義時,你會很容易認為事情不可能是隨機發生,你會相信這就是命運。我們很容易把巧合誤認成命中注定,我們很容易把運氣當成實力。從辛普森劇情中預測到川普會當總統到網路神人成功預測地震 從發現愛人與你有相同...

67.恐怖分子圖謀什麼?我們都過度重視悲劇
上次提過了“可用性”如何操弄我們的思想,今天繼續來深入探討。看看新聞媒體如何把罕見事件渲染成每天都需要防備的危險,經過不間斷地播放加深你的印象,它們為甚麼要這樣做:吸引眼球。增加電視台收視率。促使你想起人生苦短,要及時行樂(多花錢),促進經濟發展。

想得快、狠、但不准
「快思慢想」(Thinking, Fast and Slow)這本書揭露了很多關於人們使用直覺的謬誤,它的作者心理學家 Daniel Kahneman ,是2002 年的諾貝爾經濟學獎的得主。你可能會覺得奇怪,為什麼一個心理學家會得到的是經濟學獎?
在紐約確診,台北誤診
四月份的時候,住在紐約的大衛測試新冠病毒得到確診的結果,同期間另一個住在台北的大衛也得到確診的結果。兩個人都沒有出現症狀,但都被納入當地確診人口的統計數字。但是我可以告訴你,即使在已經確診的情況下,紐約的大衛其實真的有被病毒感染的機率只有 93%,而台北的大衛真的有被感染的機率更低,只有 29%。















